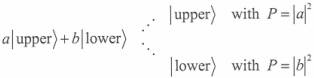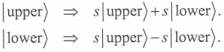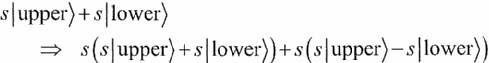1

Lecture Nine – Quantum Mechanics

States, Amplitudes, and Probabilities

Scope: The simple photon interferometer example from Lecture Eight is our doorway into the formal math of quantum theory. By learning a few symbols and a handful of rules for manipulating and interpreting them, we can describe the states of quantum particles, show how these states change over time, and predict the results of measurements. One key idea is the principle of superposition, which tells us how to combine 2 quantum states to form a new one. Another concept is the probability amplitude, used to calculate the likelihood of the various outcomes of an experiment.

Outline

I. Our aim here is to introduce a formal language to describe quantum ideas. First we introduce a few terms and abstract symbols.

A. A “system” is any piece of the quantum world that we wish to consider. For example, we might consider a single photon in an interferometer.

B. A “state” is a physical situation of some system.

1. We represent a state by a “ket,” like so: . What we put inside the ket is just a convenient label for the state

2. A “basis” is a set of distinct states that cover all of the outcomes of some measurement. For example, the photon in the interferometer would be found in one beam or the other, so the 2 states make up a basis.

3. There can be different possible measurements, so there can be different possible basis sets for a quantum system.

C. Besides “basis” states, there are also “superposition” states.

1. The term superposition is meant to suggest a composite, like 2 pictures “superimposed” on one another in a double exposure.

2. We represent a superposition as an abstract sum:

The numerical factors a and b are called “amplitudes.”

3. In full quantum mechanics, these amplitudes might include imaginary numbers . We can omit this complication, but we will use both positive and negative amplitudes.

4. We define the numbers = 0.7071 ... , for which s² = ½ (We give this number a special name for convenience because we will use it a lot in our examples.)

II. Next, we need rules for working and interpreting the abstract quantum symbols.

A. The “rule of superposition” says that a superposition of 2 or more basis states is also a quantum state.

1. The means that a quantum system has more possibilities than we might expect.

2. For the photon in the interferometer, besides and states, we also have lots of superposition states
for many different choices of amplitudes a and b.

3. A superposition state represents the photon divided among the beams in some way, as happens in an interferometer. The
amplitudes determine the details.

B. The “rule of probability” (also called the Born rule) says that if we make a measurement, the probability of any result is determined by the amplitude for that result:
probability = |ampIitude|².

1. Quantum mechanics only predicts probabilities, not definite results.

2. What is probability? For any event, its probability P is a number between 0 and 1. The value P = 0 means the event is impossible, and P = 1 means that it is certain. An intermediate value like P = 0.37 means that, if we tried the same experiment many times, the event would happen about 37% of the time. Probabilities predict statistics.

3. Both positive and negative amplitudes give positive probabilities.

4. Suppose our photon is in the state . If we make a measurement to find which beam the photon is in, we will get results with probabilities:
.
This means we must have , since probabilities must always add up to 1.

5. In the state , each beam has probability
|s|² = ½ . The same thing is also true for the different quantum
, because:

|s|²= |-s|² = ½

C. There are 2 “update rules” that tell how the state changes when something happens to the system.

1. Update rule I says that when there is no measurement, the state changes in a definite way that maintains any superposition. If we know how to update the basis states, we can determine how to update superposition states.

2. Update rule II says that when there is a measurement, we use the results to find the new state. In this case, the state is updated randomly.

3. An example for update rule II: The photon is in the , and we use photon detectors to determine which beam it is in. Then:

D. These are (almost) the only rules of quantum mechanics!

III. To understand the meaning of the quantum rules, we apply them to the photon in an interferometer.

A. At a beam splitter, the basis states change in this way:

1. This is an example of update rule I, since no measurement is made.

2. The minus sign indicates reflection from the silvered side of the mirror.

B. In the interferometer, we keep track of the quantum state at each
stage to figure out what happens to the photon.

1. The photon starts out in the upper beam, so its state is
.

2. At the first beam splitter, the state changes:
.

3. The beams recombine at the second beam splitter. We apply
the beam splitter state change to each part of the superposition,
according to update rule I:

4. We now multiply amplitudes and combine terms as we
would in an ordinary algebraic expression. This gives us the
final state:
.
At the end, the photon is certain to be in the upper beam.

5. Constructive and destructive interference take place in the
amplitudes. The quantum amplitude keeps track of the wave
properties of the photon.

Questions to Consider:

1. One of the questions for the last lecture asked what happens when the
second beam splitter is flipped so that its metal coating is on the other
side. Write down how a flipped beam splitter affects the and
basis states, and work out the final quantum state for the
photon. Does this agree with your previous answer? (It should.)

2. If we simply allow the 2 beams to cross without a beam splitter,
this simply exchanges the basis states: and
. Use this fact to find the final quantum
state if the second beam splitter is removed (as in Wheeler’s
delayed-choice experiment).